
The objective of the lesson is to give you more experience with the field and map calculator, and allow you to experiment with contouring. You will need to perform some pretty advanced operations for this lesson and you will need to think carefully about the calculations your are making. You will need to read the provide excerpt from "Whole Earth Geophysics" by Robert Lillie.
Please note that these data are preliminary and have not be quality checked.
They are for purposes of example only, and should not be distributed!
You will need to create a "gravity" directory in your user directory. Copy the file gravity.tar.gz from the /nsm/class/gly560/class/gravity/ directory into your own nsm/class/gly560/username/gravity directory. When you extract the files (using the gunzip and tar commands), it will create a rasterfiles and shapefiles directories with the following files:
Open a new view, name it "gravity survey", and change the map units to meters and the distance units to kilometers. Add the shapefiles that you find in your shapefiles directory. If you activate the themes, you should find that you have a map roads and streams in the watershed, along with the boundary of the watershed. In addition you will find maps of the surface geology as interpreted by Frimpter (1974). The attribute table contains classifications of different sediments types identified by Frimpter. Change the legend so that each sediment type has a unique color. Edit the legends of the other themes so that the colors and symbols are appropriate.
Note that the coordinates of the project are UTM Zone 17, NAD27 (i.e. METERS).
Make sure Spatial Analyst is activated, and open the 30m_DEM grid file, located
in the rasterfiles directory. This DEM file gives elevations in meters,
which is appropriate because we will want to work in SI units for this lesson.
Measured gravity readings from the Ischua Creek Valley are included in the shapefiles directory as gravity_meas_clip.shp. This name indicates that the original gravity data have been clipped such that only the data within the valley are included in the dataset. In addition, the data have been culled to reduce the number of gravity points to make the ArcView calculations go faster. Add this shapefile to your view and look at the attribute table. You should see latitude and longitude values, as well as "raw" gravity measuremnts which you will need to correct in this lab.
Save this shapefile as "gravity.shp" so that we can retain the original data set in case we break something.
Add a field called "g_t" to the gravity.shp table that represents the theoretical gravity for each survey point.
Theoretical Gravity:

The calculation can be accomplished using the field calculator, and the given latitudes for each station. The sine function in field calculator wants radians rather than degrees, so create another Number field called Lat_rad that has a width of 12 with 6 decimal places and use the .AsRadians function to convert latitude degrees to latitude radians.
Add another field called g_t (12 width 2 decimal places) for the theoretical gravity. Use the field calculator to find theoretical gravity based upon the latitude in radians. Note that the syntax for field calculations can be frustrating, so before you calculate, copy the equation using the "copy" button on your keyboard. That way if it doesn't calculate you can paste it back into the field calculator and start from there. The syntax should be, similar to this, with the use of parentheses to separate terms:
978031.85 * ( 1 + ( 0.005278895 * ( [Lat_rad].Sin ^ 2 ) ) + ( 0.000023462 * ( [Lat_rad].Sin ^ 4 ) ) )
As a check, the theoretical gravity for station #1 should be 980,373.80 mGal. If it looks OK save your edits.
To calculate free-air gravity we will need elevation. This is the tricky part because the gravity points are in a shape (vector) file, and the DEM is in a grid (raster) file. You cannot query directly between grid and shape files. We must either turn the gravity data into a grid, or the DEM into a shape file. The latter is more convenient, because that way we will not have to carry many "No Data" points in our database.
To get elevation as a shapefile we contour the DEM. Use the contour function in Spatial Analyst to contour the DEM at 3 m intervals (finer intervals will result in long computation times in the next step). Use 430 m as the base contour. Name the resulting theme "3 m Elevation Contour".
Now we want to assign the contour closest to the survey point to the record for the survey point. Thus, we want to use the Geoprocessing wizard to do a spatial join. Add the Geoprocessing extension to ArcView, highlight the gravity.shp file and activate the wizard. Choose assign data by location, and choose your gravity.shp as the table to assign data to, and the contour theme as the table to assign data from. Let the wizard to its thing, it will take a while. When it is done, open the gravity table. You should see that additional fields have been added that indicate the nearest contour line to the survey point, and the distance from the survey point to the contour. DO NOT TRY TO SAVE THE TABLE YET.
The spatial join is like any other join command, and can be removed. We will want to permanently add the elevation data to the gravity table. Add a field called "elev_m" and use the field calculator to add the contour-derived elevation. Remove the join, then save your edits. DO NOT save before removing the join, otherwise ArcView will try to do the spatial join again and you will have to wait!
We are now ready to find the Free-Air gravity anomaly. Recall that the free-air anomaly is
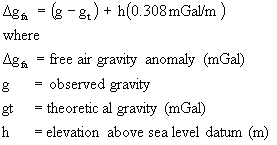
Add a field called "g_fa" to the table with 3 decimal places. Use the field calculator to calculate the free air gravity, according to the formula given above. Save the edits to your table.
As a check, the Free-Air gravity anomaly for Station #1 should be +0.396 mGal.
The final correction to the data is the Bouguer Correction. The Bouguer Correction accounts for the gravitational mass of above a datum plane, usually sea level. The objective is to remove the amount of mass that would be between the measurement elevation and sea level, such that gravity anomalies are due to DENSITY rather than elevation.
There are different Bouguer corrections applied to gentle topography, rugged topography, and sub-oceanic gravity measurements. Here, we will use the correction for gentle land topography:

Add a new field to your table "g_b" and use the field calculator to make the Bouguer correction to your data. As a check, the Bouguer anomaly for Station #1 should be -44.036.
We will want to contour the Bouguer data. Because we are looking for relatively large features (surface geology) we will want a smooth contouring of the data. The spline function is better suited for this purpose. Use the spline contouring algorithm to contour the Bouguer gravity data. You will want to test some of the options that you have for smoothing. Keep in mind that we want a surface with features of the same general scale as the surface geology. Use a 100 m cell size for contouring, or you will be waiting a while for the spline algorithm to run. The options available in the dialog box are given below.
Dialog box options:
Z value: The values being contoured. Select g_b from the list
Type: The type of curve fitting. Type can be
Regularized - Creates a smoother flowing surface.
Tension - Results in a more rough surface that tightly conforms to the input data points.
Weight: Controls the tautness of the curves. As the Weight increases with the Regularized Type, the output surface will become increasingly smoother. With the Tension Type, increasing the Weight will cause the surface to become stiffer, eventually conforming closely to the input points.
No. of Points: The number of nearest points around the cell being analyzed that will be used to fit the curve.
Notice that no matter what you do with the smoothing algorithm, it still gives outrageous contours outside of the data area. This is a characteristic of trend surfaces, where this is no data the surface trends off to unreasonable values. Once you have a surface that you are happy with, use the Geoprocessing tool to clip the contour to the boundaries of the watershed. You should find that you this produces a more pleasing contour map.
Because the data have been corrected for elevation, latitude, and mass of landforms, the changes in the gravity field are expected to be due to changes in density of the underlying material. Because the valley fill sediments are less dense than the surrounding bedrock covered by a thin mantle of till, we would expect that gravity lows would be associated with the valley fill sediments and gravity highs with the bedrock. More specifically, gravity should be inversely related to the depth of valley fill. Because we expect a linear relationship between gravity and depth of valley fill, we should be able to derive depth of sediments if we depth control at two points.
We will use two points where the depth of the surface geology is somewhat constrained. At Station 48, the thickness of the till is almost zero. At the center of the valley at Coal Chutes Road, say at Station 6, seismic data (also by Mark Saunders) indicates a depth to bedrock of approximately 100 m. The difference in the Bouguer gravity at those two points, therefore, could be interpreted to result from 100 m of overburden. We can multiply the Bouguer gravity at all the survey points by 100m/difference in Bouguer Gravity at stations 48 and 6 to get a value of thickness of overburden. Produce a contour map of overburden thickness in the watershed. After you are happy with the contouring, clip the contour to the watershed boundary as before.
Create two maps. One map should show a contour of the Bouguer Gravity Anomaly, and the other a contour of the estimate of the overburden thickness. Make sure that you use your legend editor to remove nonsense contour lines created by the spline procedure. For example, you will probably want to constrain your Bouguer data within the general range of your measured data. You also cannot have negative overburden thickness.
Make sure that you final map is properly formatted! For example, your legend should include units for gravity data and thickness. Indicate the contouring algorithm used, and the contour interval. You should have someone check over your work before handing it in.