The Error Function
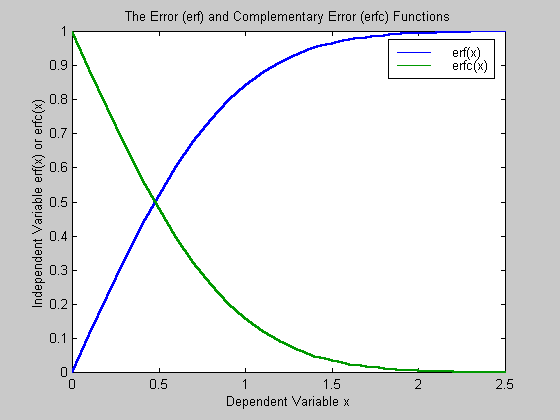
A very good description of the error function is found in Appendix 5 of Fowler. Those needing more detail are referred there but for the present purposes it is enough to know that the error function is a particular solution of the differential equations describing flow of heat or fluids. It appears so often it is given the special name of the error function and normally designated erf(x). Note that erf(0) = 0 and erf(¥ ) = 1 so it is usually scaled between two limits. The complementary error function erfc(x) = 1 -erf(x).
These two functions look like:

and the tabulated values for your reference are:
x erf(x) erfc(x)
0 0 1.0000
0.1000 0.1125 0.8875
0.2000 0.2227 0.7773
0.3000 0.3286 0.6714
0.4000 0.4284 0.5716
0.5000 0.5205 0.4795
0.6000 0.6039 0.3961
0.7000 0.6778 0.3222
0.8000 0.7421 0.2579
0.9000 0.7969 0.2031
1.0000 0.8427 0.1573
1.1000 0.8802 0.1198
1.2000 0.9103 0.0897
1.3000 0.9340 0.0660
1.4000 0.9523 0.0477
1.5000 0.9661 0.0339
1.6000 0.9763 0.0237
1.7000 0.9838 0.0162
1.8000 0.9891 0.0109
1.9000 0.9928 0.0072
2.0000 0.9953 0.0047
2.1000 0.9970 0.0030
2.2000 0.9981 0.0019
2.3000 0.9989 0.0011
2.4000 0.9993 0.0007
2.5000 0.9996 0.0004