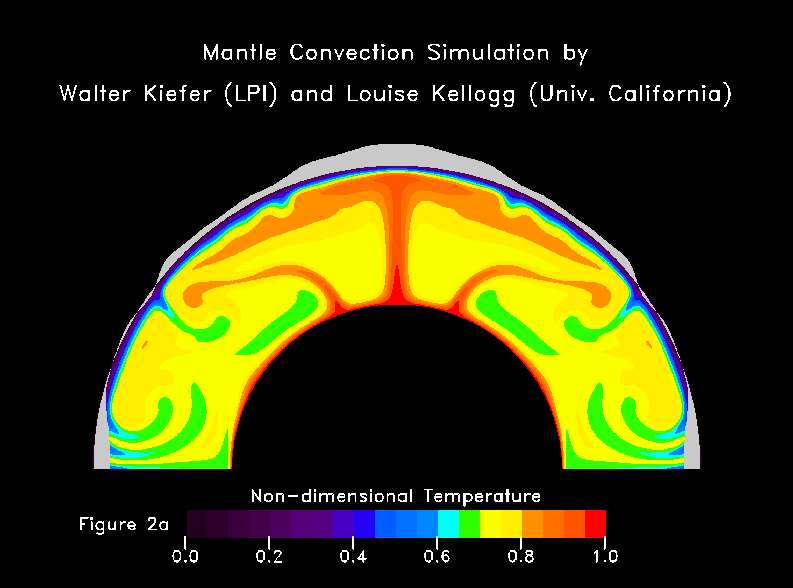
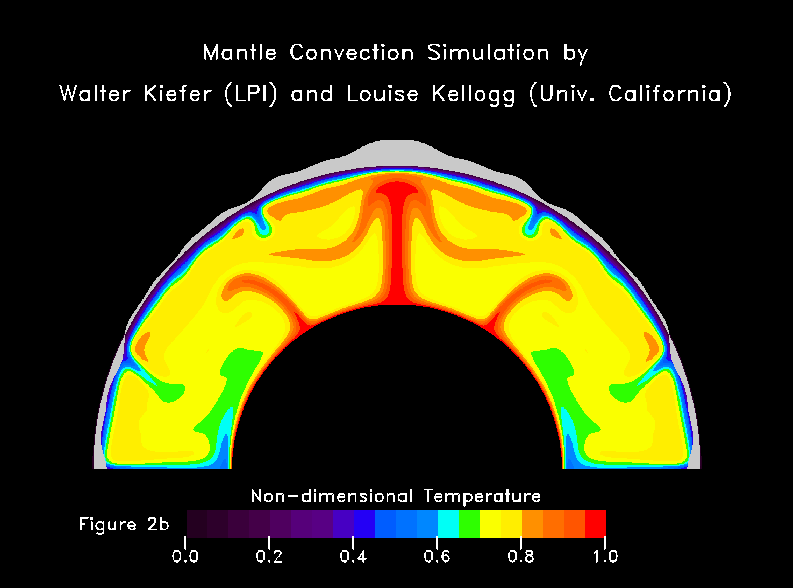
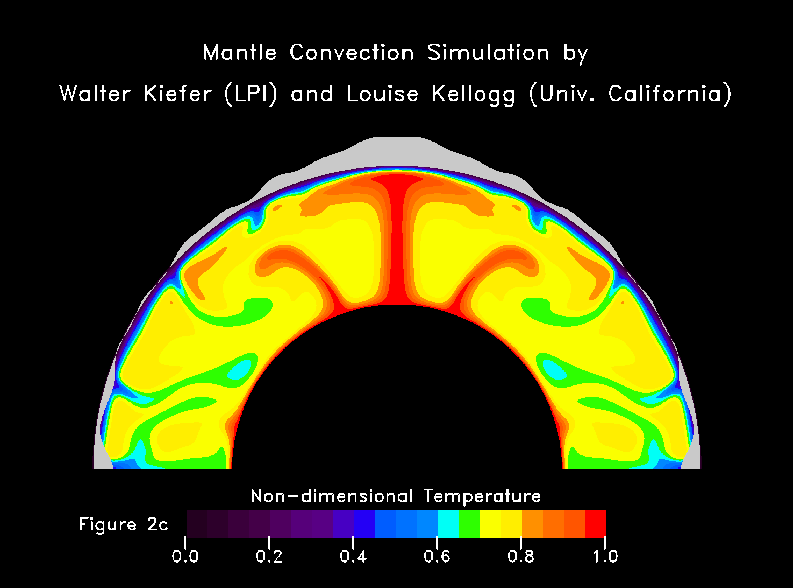
-
Geotherm: T(z,t) = erf[z/2Ö
(kt)]
What is the error function erf?
-
Heat Flow: Q(t) = -kTa/sqrt (pkt)
-
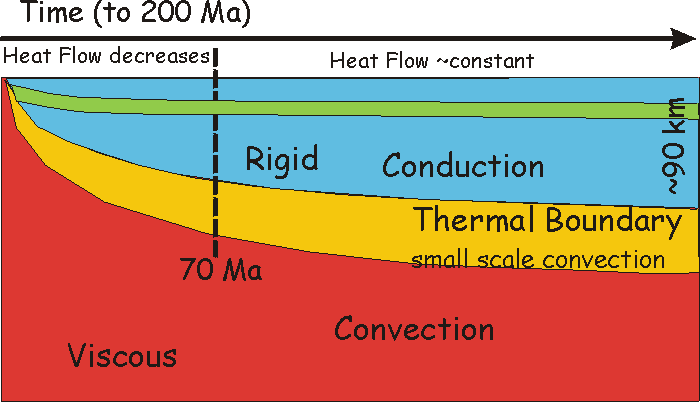
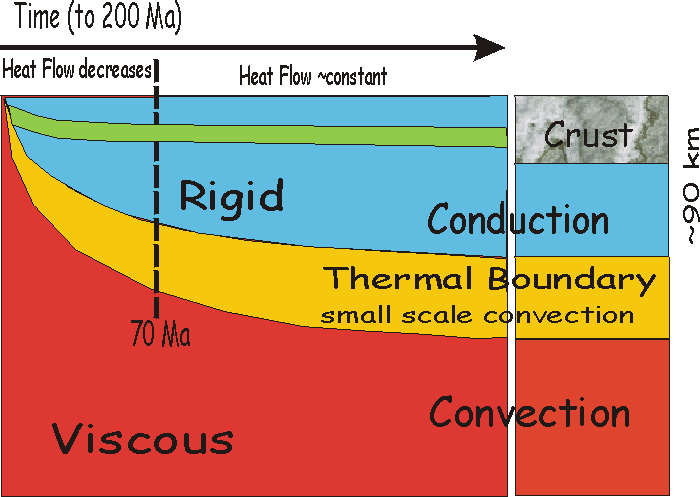
Lithospheric Thickness: Assume temperature in the asthenosphere
at the ridge axis Ta= 1300 C and the base of the lithosphere
defined by T = 1100 C. In this case one can say that L = 2.016sqrt(kt).
If k = 10-6 m2s-1
then L = 11sqrt(t) in kilometres and t in Ma then will have the following
curve but only good to about 70 Ma. After this time the lithospheric thickness
(and heat flow and ocean depth) has stabilized and come into equilibrium
with the convecting asthenosphere. Oceanic plate stays more or less the
same.
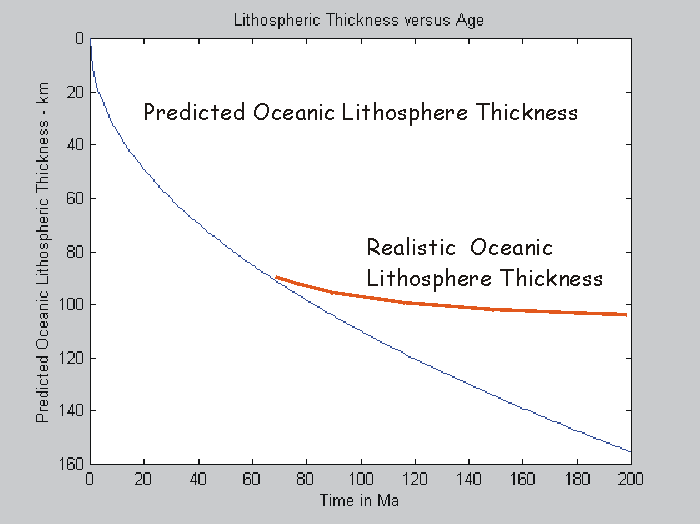
Supported by studies of surface wave dispersion.
-
Depth of the Ocean Floor with age
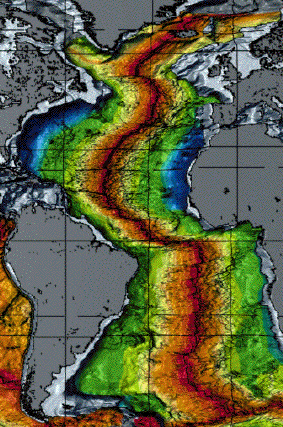
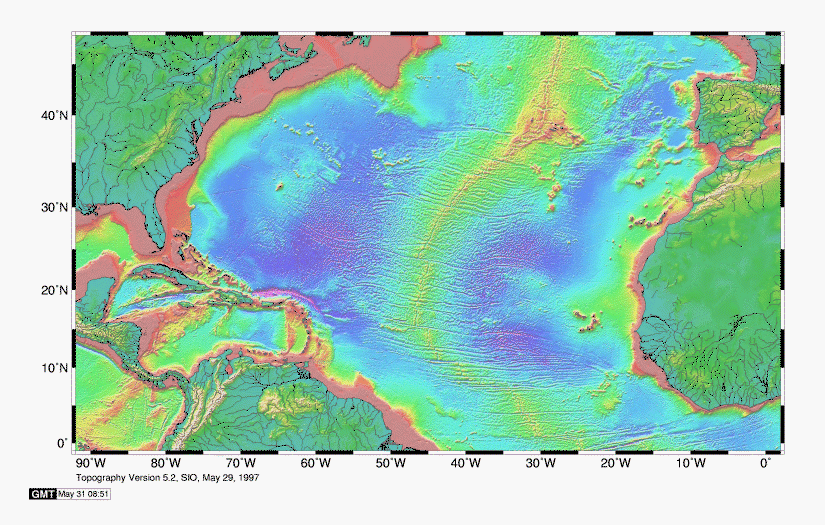
Age from MidAtlantic Ridge Topography of North Atlantic
Seafloor.
Depth stabilizes at about 70 Ma to ~5 km then increases
very slowly past this time. Effect due to increase in density from thermal
contraction as plate cools Þ density increases
with time Þ lithosphere must find new
isostatic equilibrium.
 For t < 70
Ma, d = 2.5 km + 0.35t1/2 (t in Ma) (follows Airy)
For t < 70
Ma, d = 2.5 km + 0.35t1/2 (t in Ma) (follows Airy)
 for t 70 Ma,
d = 6.4 km - 3.2exp(-t/62.8) (Lithosphere contstant - follows Pratt).
for t 70 Ma,
d = 6.4 km - 3.2exp(-t/62.8) (Lithosphere contstant - follows Pratt).
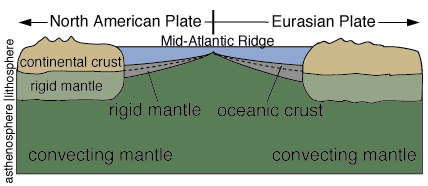
 Continental
Lithosphere
Continental
Lithosphere
 Additional
complication - continental crust contains substantial radioactive elements
- high internal heat generation.
Additional
complication - continental crust contains substantial radioactive elements
- high internal heat generation.
 Heat transmitted
primarily by conduction
Heat transmitted
primarily by conduction
 Simplest
model - plate of thickness D in which radioactive materials are presumed
to be uniformly concentrated and producing heat at a rate A overlying the
rest of the earth which inputs a constant basal heat flux Qr
Simplest
model - plate of thickness D in which radioactive materials are presumed
to be uniformly concentrated and producing heat at a rate A overlying the
rest of the earth which inputs a constant basal heat flux Qr
 At equilibrium,
T(z) = -Az2/2k + Qoz/k + Tsurface where
Qo is the observed surface heat flow.
At equilibrium,
T(z) = -Az2/2k + Qoz/k + Tsurface where
Qo is the observed surface heat flow.
 Further Qo
= Qr + AD (see Fowler, page 244)
Further Qo
= Qr + AD (see Fowler, page 244)

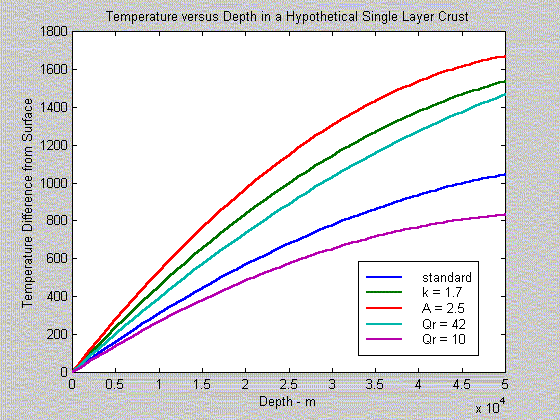
 Standard
Model: A = 1.25 mW/m3, k = 2.5 W/mC,
and Qr = 21 mW/m2 for a 50 km thickness (model after
that given by Fowler page 228).
Standard
Model: A = 1.25 mW/m3, k = 2.5 W/mC,
and Qr = 21 mW/m2 for a 50 km thickness (model after
that given by Fowler page 228).
 Continental
Lithosphere
Continental
Lithosphere
 Rigidity
of the Lithosphere
Rigidity
of the Lithosphere
Plates have the ability to bend - the static loading
by local masses will have an effect on bending and topography. This is
quantified by the
flexural rigidity D = Eh3/12(1
- n2),
h = thickness, E = Young's modulus, n
= Poisson's ratio (see seismic lectures for definitions of these
elastic parameters). Units of
D are Nm = bending moment. D is a fundamental parameter describing the
plate - it tells how much it will resist bending.
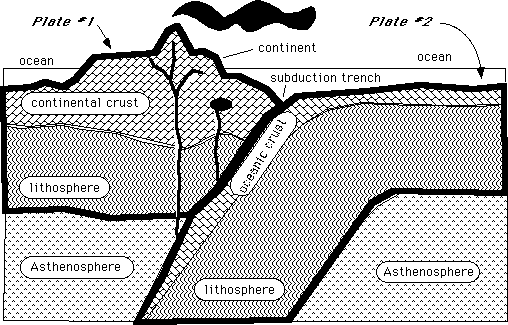
Some examples of this include:
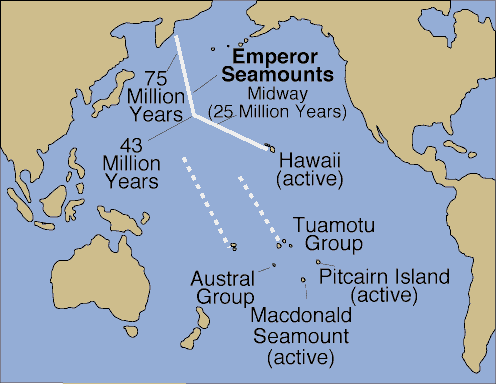
 Loading by Oceanic Islands
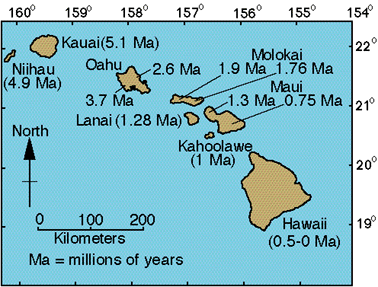
Loading by Oceanic Islands 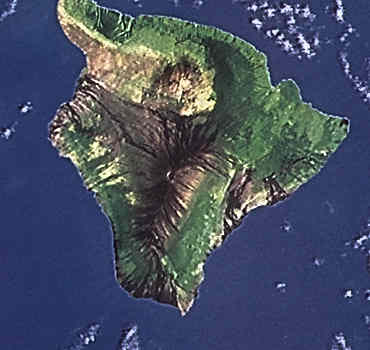 Big island of Hawaii from space
Big island of Hawaii from space
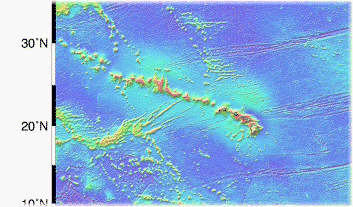 Note zone
of deepening near big Island - also increased topography leading up to
it due to increased heat in mantle (see hot spots a little later).
Note zone
of deepening near big Island - also increased topography leading up to
it due to increased heat in mantle (see hot spots a little later).
Principal Idea shown in the cartoon below
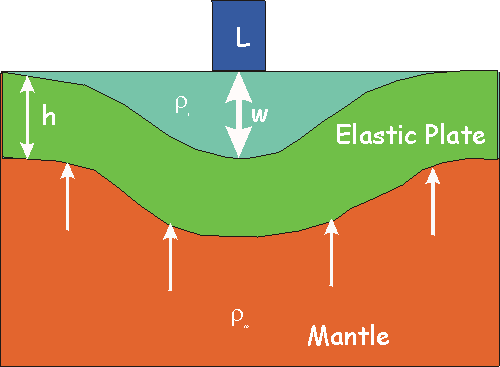
L is the load (in terms of Force/area), rmis
the density of the mantle, riis
the density of the material infilling the depression.
L pushes down but is balanced by elastic deformation of the plate and
bouyancy according to Archimedes of gw(rm
- ri).
Complex solution in elasticity but result is:
-
w(x) = woexp(-x/a)[cos(x/a)
+ sin(x/a)] where
-
wo = La3/8D
is the maximum deflection beneath the load L
-
a = [4D/(rm
- ri)g]1/4
is called the flexural parameter.
![]() Kelvin Scale
- begins at absolute zero. Water triple point at 273.16 K.
Kelvin Scale
- begins at absolute zero. Water triple point at 273.16 K.

![]() Celsius - same
units as Kelvin - Water triple point @ 0 C.
Celsius - same
units as Kelvin - Water triple point @ 0 C.![]() Joule - Amount
of energy required to push with a force of 1 Newton for 1 meter. 1 Calorie
= 4.1868 J.
Joule - Amount
of energy required to push with a force of 1 Newton for 1 meter. 1 Calorie
= 4.1868 J.
![]() Watt - Unit
of power. 1 Watt = 1 Joule/second
Watt - Unit
of power. 1 Watt = 1 Joule/second
![]() Heat Flux (Flow):
amount of energy flowing through an area in a given time. In geophysics,
typical SI unit = mW/m2. Old units are 'Heat Flow Units' = HFU
= 1 mcal/cm2/sec = 41.9 mW/m2
Heat Flux (Flow):
amount of energy flowing through an area in a given time. In geophysics,
typical SI unit = mW/m2. Old units are 'Heat Flow Units' = HFU
= 1 mcal/cm2/sec = 41.9 mW/m2 Diamond
film cutting through an ice crystal due to thermal conduction from the
person's fingers
Diamond
film cutting through an ice crystal due to thermal conduction from the
person's fingers







 Big island of Hawaii from space
Big island of Hawaii from space
 Note zone
of deepening near big Island - also increased topography leading up to
it due to increased heat in mantle (see hot spots a little later).
Note zone
of deepening near big Island - also increased topography leading up to
it due to increased heat in mantle (see hot spots a little later).

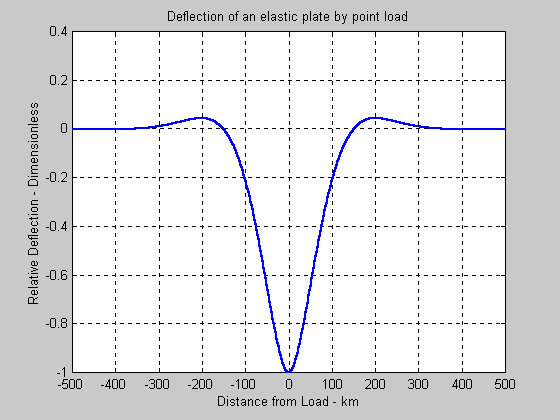
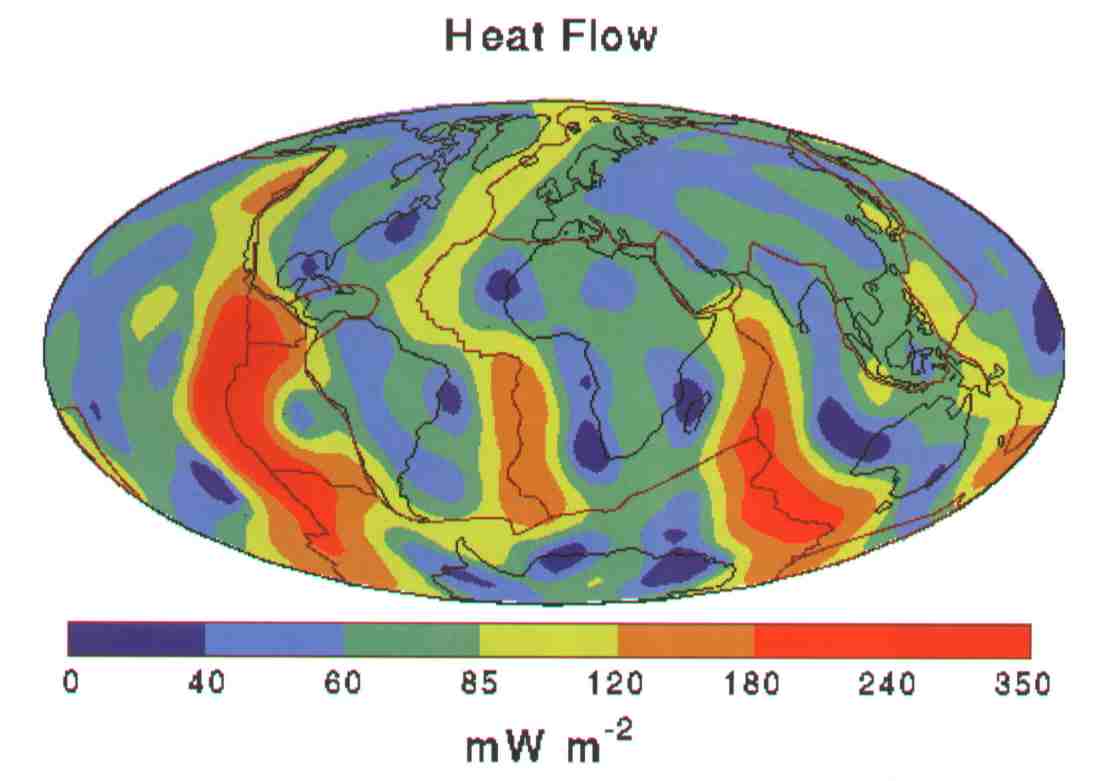
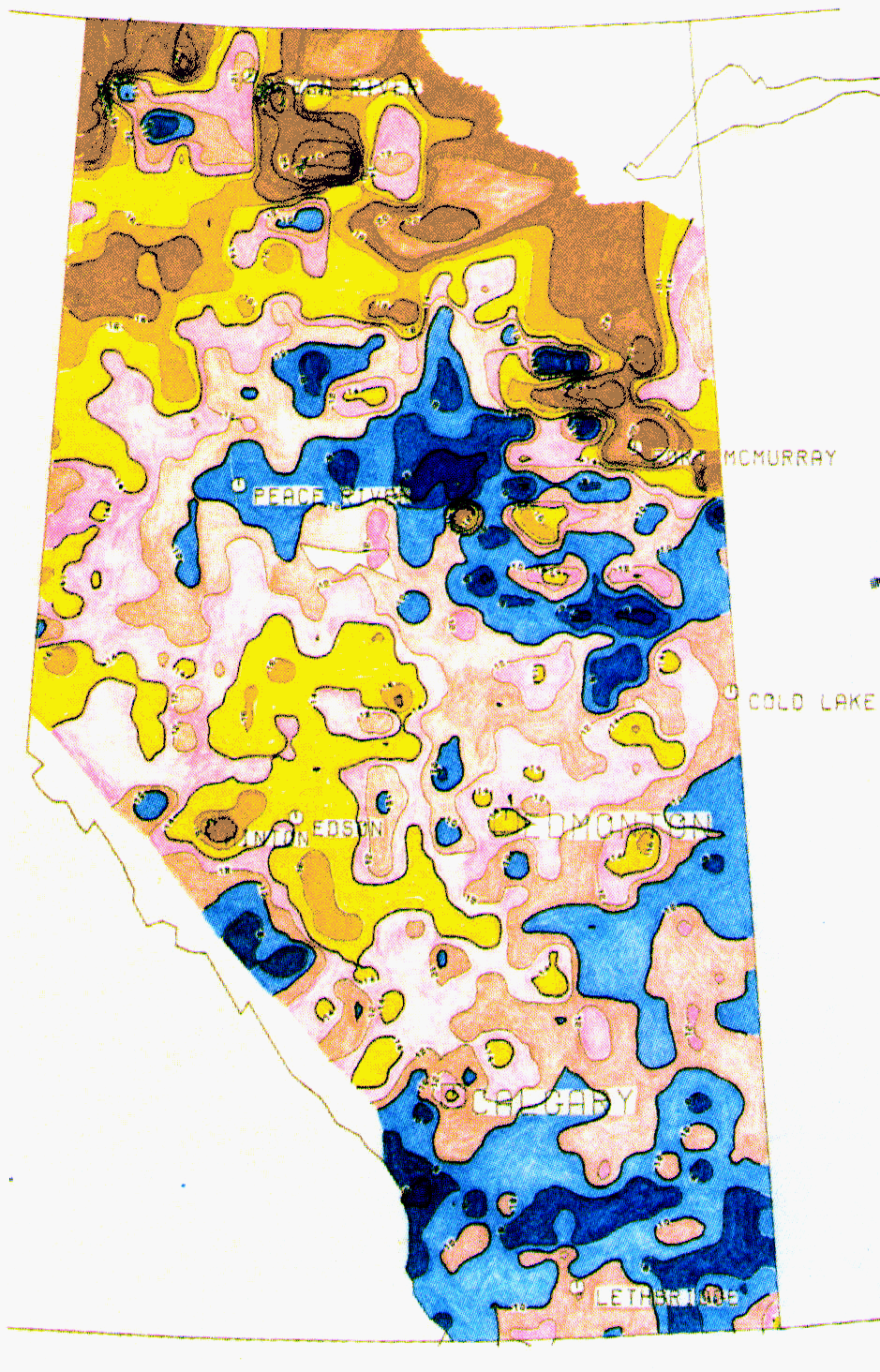 Image by
Dr. Walter Jones and colleagues, U of Alberta - report on geothermal potential
in Alberta
Image by
Dr. Walter Jones and colleagues, U of Alberta - report on geothermal potential
in Alberta